Pi is the ratio of the circumference of a circle to its diameter.
It is a constant. The familiar value is 3.14159.
It is irrational – it cannot be written as a fraction using 2 integers, although, some approximations, like 22 / 7, are used.
It is transcendental – this means there is no algebraic equation for which it is the solution (algebraic equations look like this: x2 – 2 = 0 or x2 – x – 1 = 0 or 8x3 – 3 = 0), or, as Euler is claimed to have said, “They transcend algebra”.
The relationship between the circumference of a circle and its diameter has been known for thousands of years. The Babylonians knew it, as did the ancient Egyptians and the ancient Greeks – although, it wasn’t called Pi back then. The symbol π and the name Pi were introduced William Jones in 1706 – previously, it was always referred to as “the ratio between the circumference of a circle to its diameter”. The symbol π is taken from the first letter of the Greek word perimetros (περιμετρος) – for the perimeter (or circumference) of a circle (circumference comes from a Latin root, whereas perimeter comes from a Greek root).
Had Julius Caesar not managed to burn down the Library of Alexandria in 48BCE, our knowledge of ancient history, culture, mathematics and science would likely be more complete. As it stands, our knowledge is fragmentary, but it is pretty obvious that the ancients were curious about the world around them and sought to understand it (just as people do today).
One of the things they discovered was that the length of the edge of a circle (its circumference or perimeter) was always a little more than 3 times the length of the diameter of the circle. The ancient Egyptians estimated it at 256 / 81 (written in some texts as 4 x (8 / 9)2). Archimedes narrowed down the value to being somewhere between 3 + 10 / 71 and 3 + 1 / 7 (or 223 / 71 and 22 / 7).
In mathematical notation we would write down Archimedes’ range as:
223 / 71 ≤ π ≤ 22 / 7
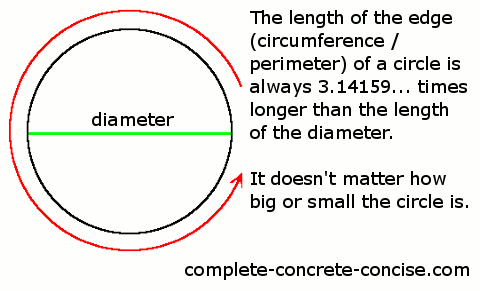
It doesn’t matter how big or small the circle is, the length of the edge is always 3.14159… times longer than its diameter.
The ratio of the circumference to the diameter is not the only relationship we can find in a circle. There is also the ratio of the circumference to the radius (which leads to the concept of the radian) and the ratio of the diameter to the radius.
The ratio of the circumference to the radius is 6.28318… (or 2π). It doesn’t matter how big or small the circle is, the length of the edge (circumference or perimeter) of the circle will always be a little more than 6 times the length of the radius. (If mathematicians had been using the ratio of the circumference to the radius, then the value of π would have been 6.28318… instead of the familiar 3.14159…)
The ratio of the diameter to the radius is 2. Again, it doesn’t matter how big or small the circle is, the length of the diameter will always be twice as long as the length of the radius. (Let’s be thankful that we use the symbol 2 for this instead of some Greek letter, like ζ)
Empirically determining the value of Pi
You can do a simple experiment to determine the value of Pi:
- Get a round cardboard tube (one that is reasonably round and not squished too much – a toilet paper roll is fine).
- Measure the diameter of the tube using a ruler (it’s a good idea to take several different measurements across the tube and average them out).
- Cut the tube lengthwise with a pair of scissors.
- Lay the cut tube flat and measure the width.
- Divide the width of the flat tube by the diameter of the tube.
When I did this, I got a diameter of 38mm and a width of 118.4mm:
118.4 / 38.0 = 3.116 – a reasonably close empirical value for Pi.
Another experiment is:
- Get something round (a tin can, a plastic tub, a CD, a roll of tape).
- Measure the diameter of the object.
- Make a small mark on the edge of the object.
- Put the object, mark down, on a sheet of paper.
- Mark the position on the paper.
- Carefully roll the object along the paper until the mark once again touches the paper. (This “unrolls” the length of the edge on the paper)
- Mark that position on the paper.
- Measure the distance between the two marks.
- Divide the distance between the two marks (which is equal to the length of the edge of the round object) by the diameter of the object.
Using a CD, I measured a diameter of 120mm and a distance of 376.8mm:
376.8 / 120 = 3.14 – I think I was just lucky to have rolled out the CD so accurately).
Alternately, if you have a roll of masking tape:
- Using a sharp knife, cut through several layers of the tape (at least two).
- Measure the diameter of the roll.
- Pull off a strip of tape (since the tape is cut, you will only be able to pull off a length equal to the circumference of the roll – well, the first strip might be shorter, so discard it).
- Carefully stick the strip to a piece of paper.
- Measure the length of the strip.
- Divide the length of the strip by the diameter of the roll.
The diameter of my roll of masking tape was 127.7mm and the length of the strip of tape was 401.5mm:
401.5 / 127.8 = 3.144 – another very close empirical measurement.
If you have a tape measure (not the metal kind), then you can wrap the tape measure around the circumference of the round object and measure the length of the edge that way.
Wow! That’s an exciting slant.
Uhm … ok … exciting wasn’t exactly what I had in mind – more like “interesting” or maybe “Oh! Now I get it.”